For FieldFamilys for which the
api_extensions POLY is implemented, which
are every one for the moment, there are three more types.
typedef mpfq_TAG_poly;
typedef mpfq_TAG_dst_poly;
typedef mpfq_TAG_src_poly;
To manipulate objects of one of these types, one can use the following functions.
/* Element allocation functions */
void mpfq_TAG_poly_init(mpfq_TAG_dst_field, mpfq_TAG_poly, unsigned int);
void mpfq_TAG_poly_clear(mpfq_TAG_dst_field, mpfq_TAG_poly);
/* Element assignment functions */
void mpfq_TAG_poly_set(mpfq_TAG_dst_field, mpfq_TAG_dst_poly, mpfq_TAG_src_poly);
void mpfq_TAG_poly_setmonic(mpfq_TAG_dst_field, mpfq_TAG_dst_poly, mpfq_TAG_src_poly);
void mpfq_TAG_poly_setcoef(mpfq_TAG_dst_field, mpfq_TAG_dst_poly, mpfq_TAG_src_poly, unsigned int);
void mpfq_TAG_poly_setcoef_ui(mpfq_TAG_dst_field, mpfq_TAG_dst_poly, unsigned long, unsigned int);
void mpfq_TAG_poly_getcoef(mpfq_TAG_dst_field, mpfq_TAG_dst_elt, mpfq_TAG_src_poly, unsigned int);
void mpfq_TAG_poly_random(mpfq_TAG_dst_field, mpfq_TAG_dst_poly, unsigned int, gmp_randstate_t);
void mpfq_TAG_poly_random2(mpfq_TAG_dst_field, mpfq_TAG_dst_poly, unsigned int, gmp_randstate_t);
/* Arithmetic operations on elements */
void mpfq_TAG_poly_add(mpfq_TAG_dst_field, mpfq_TAG_dst_poly, mpfq_TAG_src_poly, mpfq_TAG_src_poly);
void mpfq_TAG_poly_sub(mpfq_TAG_dst_field, mpfq_TAG_dst_poly, mpfq_TAG_src_poly, mpfq_TAG_src_poly);
void mpfq_TAG_poly_add_ui(mpfq_TAG_dst_field, mpfq_TAG_dst_poly, mpfq_TAG_src_poly, unsigned long);
void mpfq_TAG_poly_sub_ui(mpfq_TAG_dst_field, mpfq_TAG_dst_poly, mpfq_TAG_src_poly, unsigned long);
void mpfq_TAG_poly_neg(mpfq_TAG_dst_field, mpfq_TAG_dst_poly, mpfq_TAG_src_poly);
void mpfq_TAG_poly_scal_mul(mpfq_TAG_dst_field, mpfq_TAG_dst_poly, mpfq_TAG_src_poly, mpfq_TAG_src_elt);
void mpfq_TAG_poly_mul(mpfq_TAG_dst_field, mpfq_TAG_dst_poly, mpfq_TAG_src_poly, mpfq_TAG_src_poly);
void mpfq_TAG_poly_divmod(mpfq_TAG_dst_field, mpfq_TAG_dst_poly, mpfq_TAG_dst_poly, mpfq_TAG_src_poly, mpfq_TAG_src_poly);
void mpfq_TAG_poly_precomp_mod(mpfq_TAG_dst_field, mpfq_TAG_dst_poly, mpfq_TAG_src_poly);
void mpfq_TAG_poly_mod_pre(mpfq_TAG_dst_field, mpfq_TAG_dst_poly, mpfq_TAG_src_poly, mpfq_TAG_src_poly, mpfq_TAG_src_poly);
The function divmod implements, for now, the basic
algorithm for the Euclidiean division. The functions
precomp_mod and mod_pre are related to
another algorithm for the Euclidean division.
precomp_mod(K,Q,P) computes the inverse of
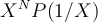modulo 
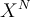, and puts it in Q,
where N is the degree of P. It requires that P be a monic polynomial
over the field K. mod_pre(K,R,Q,P,invrevP) computes the
reminder of the Euclidean division of Q by P and puts it in R,
provided that invrevP is the inverse of 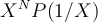modulo
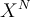, where N is the degree of P. For more information,
one can read chapter 9 of Modern Computer Algebra from Joachim von
zur Gathen and Jürgen Gerhard, and in particular Algotihm 9.5.
/* gcd functions */
void mpfq_TAG_poly_gcd(mpfq_TAG_dst_field, mpfq_TAG_dst_poly, mpfq_TAG_src_poly, mpfq_TAG_src_poly);
void mpfq_TAG_poly_xgcd(mpfq_TAG_dst_field, mpfq_TAG_dst_poly, mpfq_TAG_dst_poly, mpfq_TAG_dst_poly, mpfq_TAG_src_poly, mpfq_TAG_src_poly);
/* Comparison function */
int mpfq_TAG_poly_cmp(mpfq_TAG_dst_field, mpfq_TAG_src_poly, mpfq_TAG_src_poly);
int mpfq_TAG_poly_deg(mpfq_TAG_dst_field, mpfq_TAG_src_poly);
/* Input/output functions */
void mpfq_TAG_poly_asprint(mpfq_TAG_dst_field, char**, mpfq_TAG_src_poly);
void mpfq_TAG_poly_fprint(mpfq_TAG_dst_field, FILE*, mpfq_TAG_src_poly);
void mpfq_TAG_poly_print(mpfq_TAG_dst_field, mpfq_TAG_src_poly);
int mpfq_TAG_poly_sscan(mpfq_TAG_dst_field, mpfq_TAG_dst_poly, const char*);
int mpfq_TAG_poly_fscan(mpfq_TAG_dst_field, FILE*, mpfq_TAG_dst_poly);
int mpfq_TAG_poly_scan(mpfq_TAG_dst_field, mpfq_TAG_dst_poly);